POSICIÓN RELATIVA DE DOS RECTAS EN EL PLANO

Read More

ECUACIONES PARAMETRICAS

Unidad N° 2

Ecuaciones paramétricas de la recta conocidos un punto y un vector director

Las ecuaciones paramétricas de cualquier recta r se obtienen por medio de la siguiente expresión:

{x=a1+λ⋅v1y=a2+λ⋅v2  λ∈R

Donde:

• x e y son las coordenadas de cualquier punto P(x,y) de la recta.
• a1 y a2 son las coordenadas de un punto conocido de la recta A(a1,a2).
• v1 y v2 son las componentes de un vector director v→=(v1,v2) de r.
• λ es un valor real que determina cada coordenada P(x,y) dependiendo del valor que se le asigne.

Explicación

Cualquier recta r que puedas dibujar sobre una hoja de papel puede ser determinada analíticamente por medio de punto A que forme parte de dicha recta y una dirección que se puede expresar mediante un vectorno nulo v→ .

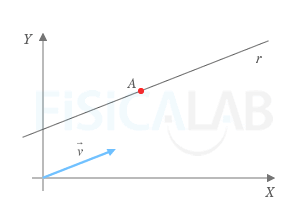
Definición de una recta por medio de un punto y un vector

Como puedes observar en la figura r se trata de una recta que pasa por el punto A y cuya dirección viene dada por el vector v→.

El vector encargado de determinar la dirección de la recta recibe el nombre de vector director y como podrás imaginar este no es único ya que cualquier vector paralelo a este nos sirve también para determinar la dirección de la recta. De esta forma, si v→ es un vector director de la recta r, también lo serán cualquier múltiplo de v→ (λ⋅v→   λ∈R).

Multiplicación de un número real por un vector cualquiera

Observa en la figura como al multiplicar el vector a→ por un número real este no cambia de dirección, aunque si lo puede hacer en módulo (tamaño) o en sentido (si el número es negativo). De forma básica para definir una recta es necesaria la dirección de un vector (no su módulo o sentido). Por tanto, si utilizamos el vector a→ para definir una recta en realidad podemos utilizar cualquier vector que cumpla que λ⋅a→   λ∈R, ya que todos tienen la misma dirección.

Tal y como estudiamos en la ecuación vectorial de una recta, si A(a1,a2) es un punto conocido de una recta r que posee un vector director v→=(v1,v2) y P(x,y) un punto cualquiera de ella sabemos que:

(x,y)=(a1,a2)+λ(v1,v2)    λ∈R

De aquí podemos deducir que:

(x,y)=(a1+λ⋅v1,a2+λ⋅v2)    λ∈R

Si a continuación igualamos las componentes a uno y otro lado de la ecuación obtenemos lo que se denominan ecuaciones paramétricas de la recta.

{x=a1+λ⋅v1y=a2+λ⋅v2  λ∈R

Read More